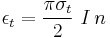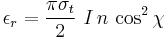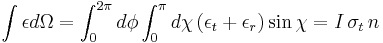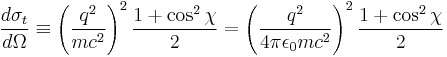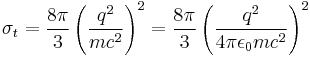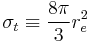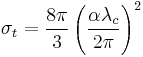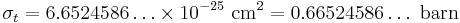Thomson scattering

Thomson scattering is the elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is just the low-energy limit of Compton scattering: the particle kinetic energy and photon frequency are the same before and after the scattering. This limit is valid as long as the photon energy is much less than the mass energy of the particle: 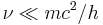\nu\ll mc^2/h .

Contents

Introduction

In the low-energy limit, the electric field of the incident wave (photon) accelerates the charged particle, causing it, in turn, to emit radiation at the same frequency as the incident wave, and thus the wave is scattered. Thomson scattering is an important phenomenon in plasma physics and was first explained by the physicist J.J. Thomson. As long as the motion of the particle is non-relativistic (i.e. its speed is much less than the speed of light), the main cause of the acceleration of the particle will be due to the electric field component of the incident wave, and the magnetic field can be neglected. The particle will move in the direction of the oscillating electric field, resulting in electromagnetic dipole radiation. The moving particle radiates most strongly in a direction perpendicular to its motion and that radiation will be polarized along the direction of its motion. Therefore, depending on where an observer is located, the light scattered from a small volume element may appear to be more or less polarized.

The electric fields of the incoming and observed beam can be divided up into those components lying in the plane of observation (formed by the incoming and observed beams) and those components perpendicular to that plane. Those components lying in the plane are referred to as "radial" and those perpendicular to the plane are "tangential", since this is how they appear to the observer.

The diagram on the right is in the plane of observation. It shows the radial component of the incident electric field causing a component of motion of the charged particles at the scattering point which also lies in the plane of observation. It can be seen that the amplitude of the wave observed will be proportional to the cosine of χ, the angle between the incident and observed beam. The intensity, which is the square of the amplitude, will then be diminished by a factor of cos2(χ). It can be seen that the tangential components (perpendicular to the plane of the diagram) will not be affected in this way.

The scattering is best described by an emission coefficient which is defined as ε where ε dt dV dΩ dλ is the energy scattered by a volume element 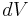dV in time dt into solid angle dΩ between wavelengths λ and λ+dλ. From the point of view of an observer, there are two emission coefficients, εr corresponding to radially polarized light and εt corresponding to tangentially polarized light. For unpolarized incident light, these are given by:

\epsilon_t = \frac{\pi \sigma_t }{2}~I\,n
\epsilon_r = \frac{\pi \sigma_t }{2}~I\,n\,\cos^2\chi

where n is the density of charged particles at the scattering point, I is incident flux (i.e. energy/time/area/wavelength) and 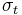\sigma_t is the Thomson cross section for the charged particle, defined below. The total energy radiated by a volume element 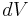dV in time dt between wavelengths λ and λ+dλ is found by integrating the sum of the emission coefficients over all directions (solid angle):

\int\epsilon d\Omega = \int_0^{2\pi}d\phi \int_0^\pi d\chi \left(\epsilon_t%2B\epsilon_r\right) \sin \chi = I\,\sigma_t\,n

The Thomson differential cross section, related to the sum of the emissivity coefficients, is given by

\frac{d\sigma_t}{d\Omega} \equiv \left(\frac{q^2}{mc^2}\right)^2\frac{1%2B\cos^2\chi}{2} = \left(\frac{q^2}{4\pi\epsilon_0mc^2}\right)^2\frac{1%2B\cos^2\chi}{2}

where the first expression is in cgs units, the second in SI units; q is the charge per particle, m the mass of particle, and 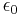\epsilon_0 a constant, the permittivity of free space. Integrating over the solid angle, we obtain the Thomson cross section (in cgs and SI units):

\sigma_t = \frac{8\pi}{3}\left(\frac{q^2}{mc^2}\right)^2=\frac{8\pi}{3}\left(\frac{q^2}{4\pi\epsilon_0mc^2}\right)^2

The important feature is that the cross section is independent of photon frequency. Note that the cross section is simply proportional (by a numerical factor) to the square of the classical radius of a point particle of mass m and charge q:

\sigma_t \equiv \frac{8\pi}{3}r_e^2

Alternatively, this can be seen in terms of 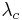\lambda_c, the Compton wavelength, and the fine structure constant:

\sigma_t = \frac{8 \pi}{3} \left(\frac{\alpha \lambda_c}{2\pi}\right)^2

For an electron, the Thomson cross-section is numerically given by:

\sigma_t =6.6524586\ldots\times 10^{-25}~\textrm{cm}^2=0.66524586\ldots~\textrm{barn}

Examples of Thomson scattering

The cosmic microwave background is thought to be linearly polarized as a result of Thomson scattering. Probes such as WMAP and the current Planck mission attempt to measure this polarization.

The solar K-corona is the result of the Thomson scattering of solar radiation from solar coronal electrons. NASA's STEREO mission will generate three-dimensional images of the electron density around the sun by measuring this K-corona from two separate satellites.

In tokamaks and other experimental fusion devices, the electron temperatures and densities in the plasma can be measured with high accuracy by detecting the effect of Thomson scattering of a high-intensity laser beam.

Inverse-Compton scattering can be viewed as Thomson scattering in the rest frame of the relativistic particle.

See also

References

External links

Effects
Full-sky temperature map taken by NASA's Wilkinson Microwave Anisotropy Probe (WMAP)
Space-based
experiments
Balloon
experiments
Ground-based
experiments